Exam 10 Dos leyes integrales de magnetismo

CARBAJAL ESCALONA SILVIA BERENICE 

EXAMENES 9 D Y 9 E Dos Leyes Integrales de Electricidad

CARBAJAL ESCALONA SILVIA BERENICE 

Exam 9 Integral definitivo

CARBAJAL ESCALONA SILVIA BERENICE

9 A. ¿COMO SE DEFINE CONCEPTO DE INTEGRAL [DEFINITIVO] EN BACHILLERATO?

La integral definida es un concepto utilizado para determinar el valor de las áreas limitadas por curvas y rectas. Dado el intervalo [a, b] en el que, para cada uno de sus puntos x, se define una función f (x) que es mayor o igual que 0 en [a, b], se llama integral definida de la función entre los puntos a y b al área de la porción del plano que está limitada por la función, el eje horizontal X y las rectas verticales de ecuaciones x = a y x = b.

La integral definida de la función entre los extremos del intervalo [a, b] se denota como:

9 B. INCRUSTACIÓN 

Al hablar de incrustacion nos referimos a trazar un plano con dos dimensiones, desde pequeños nos enseñan que estas dos dimensiones se llaman "x" y "y" y las cuales se cruzan en un punto (0,0), como a continuación se ilustra:

La incrustacion de dimensiones aprendidas desde pequeños es errónea puesto que cualquier dimensión que sea trazada en un plano no tendrá un mismo punto de partida con la otra dimensión, puesto que se habla de dos dimensiones diferentes. En este caso se habla de "x" que es un punto de curva y de "y" que es curvas de nivel. 

LO CORRECTO ES INCRUSTAR las dimensiones dentro del plano como se muestra:

9 C Presentar su lista privada de los conceptos desde mas importantes para
esta asignatura de TEORIA de Electricidad y Magnetismo.

1°ORIENTACION. Porque sin orientacion no hay borde.

2° BORDE: Sin borde no hay integral 

3° Diferencial: d

4° Integral 

EXAMENES 7 C Y 7 D

CARBAJAL ESCALONA SILVIA BERENICE.

7  C  COMO DEFINEN EL CONCEPTO DE DIFERENCIAL:

 en matematicas:

Sea una funcion y=f(x).

se define como la diferencial de la variable independiente a:

 Se define como la diferencial de la variable dependiente a :

 Esto significa que la diferencial de la variables es por definición igual al incremento que experimenta, sin embargo, la diferencial de la variable no es igual a su incremento.

7 D DECAIMIENTO DE BETA

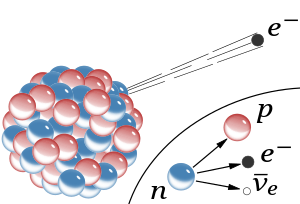
El decaimiento de beta es un proceso mediante el cual un nucleido o núcleo inestable emite una partícula beta (un electrón o positron) para compensar la relación de neutrones y protones del núcleo atómico.
Cuando esta relación es inestable, algunos neutrones se convierten en protones. Como resultado de esta mutación, cada neutron emite una partícula beta y un antineutrino electrónico.

La partícula beta puede ser un electrón, en una emisión beta menos (β–), o un positrón, en una emisión beta más (β+). La diferencia fundamental entre un electrón (β–) y la de un positrón (β+) con respecto a la partícula beta correspondiente es el origen nuclear de aquéllos: no se trata de un electrón ordinario expulsado de un orbital atómico.

En este tipo de desintegración, el número de neutrones y protones, o número másico, permanece estable, ya que la cantidad de neutrones disminuye una unidad y la de protones aumenta así mismo una unidad. El resultado del decaimiento beta es un núcleo en que el exceso de neutrones o protones se ha corregido en dos unidades y por tanto resulta más estable.

7 A y B

CARBAJAL ESCALONA SILVIA BERENICE 

7 A. Dar su ejemplo de curvas de niveles

Es necesario saber  ¿que es una curva de nivel?

Las curvas de nivel son aplicadas en el área de la Ingeniería para mostrar en el plano curvas isotermas o líneas equipotenciales, por mencionar algunas. En las curvas Isotermas la líneas continuas enlazan la misma temperatura en la zona. 

DEFINICIÓN    Curva de nivel

El conjunto de puntos (x, y) en el plano donde una función de dos variables independientes tiene un valor constante f(x, y) = c, es una curva de nivel de f.

Ejemplo Trazar algunas curvas de nivel de la función , para 

c = –1,        c = 1               y      c = 4

Solución  La función dada representa la superficie de un paraboloide elíptico abierto hacia arriba.  Si (x, y) = (0, 0)  entonces z = –5.   Las curvas de nivel son elipses.

7 B. Presentar su privado ejemplo de evaluacion gra camente de un campo
vectorial (de
echas) con una forma-onda (con crestes) en tres puntos.

CORRECIÓN 3D. BORDE NO TIENE BORDE. DEFINICIÓN DE INTEGRAL

CARBAJAL ESCALONA SILVIA BERENICE 

En el bachillerato nos muestran la definición de integral como:

 

LA DEFINICIÓN CORRECTA DE LA INTEGRAL ES:

CADA VEZ QUE SE INTEGRA SOBRE "BORDE DE ALGO" EL BORDE PASA HACER DIFERENCIAL. 

Axioma de calculo integral: borde no
tiene borde.

El borde (limite, frontera,etc.) no puede tener un borde puesto que disminuye la dimensión y es por esta razón que siempre que se tenga borde de borde, diferencial de diferencial sera cero. 

6 B. Reglas de Leibniz.

CARABAJAL ESCALONA SILVIA BERENICE 

La regla del producto es simple: Se tiene:  —> donde f(x) es cualquier función y g(x) también.

 La regla es la siguiente:

 

La derivada de el producto de dos números es igual a el primero por la derivada del segundo más el segundo por la derivada del primero.

ejemplo:

6 A Ejemplo personal de diferentes derivadas en función de las diferentes direcciones de vectores

 CARBAJAL ESCALONA SILVIA BERENICE 

EJEMPLO PERSONAL:

Tenemos una función derivable:

la cual se pide derivar en diferentes direcciones:

como se puede observar al derivar en diferentes direcciones aunque se tenga la misma función para hacerlo el resultado sera diferente en cada caso. 

CON LO CUAL SE LLEGA A LA CONCLUSIÓN QUE PARA REALIZAR LA DERIVACIÓN DE UNA FUNCIÓN ES SIEMPRE NECESARIO LA DIRECCIÓN DE LA DERIVADA PUESTO QUE SIN ESTA SERA IMPOSIBLE REALIZAR LA DERIVACIÓN. 

EXAMEN 6.ESCALARES Y VECTORES. DERIVADA Y DIRECCIÓN.

CARBAJAL ESCALONA SILVIA BERENICE 

ESCALARES

Son magnitudes que quedan determinadas con un solo numero real y una unidad de medida, se les puede representar como segmentos tomados sobre una recta a partir de un origen y de longitud igual al numero real que indica su medida. Ejemplos de magnitudes vectoriales: volumen, temperatura, el trabajo. En termodinámica, una  variable termodinámica es  función de estado, y no se utiliza nombre de campo escalar. Un campo escalar es sinónimo de una función real el cual se debe visualizar gráficamente como curvas, superficies y volúmenes de los niveles.

VECTORES

Se llama vector a todo segmento orientado. El primero de los puntos que lo determinan se llama origen y el segundo extremo. La recta que contiene el vector determina la DIRECCIÓN del mismo y la orientación sobre la recta.

EN CALCULO:

Si a cada punto de una región del espacio (x,y,z) le asociamos un escalar (número), función de la posición U(x,y,z), hemos definido un campo escalar, donde la  función U depende exclusivamente del punto que consideremos. A dicha función  U(x,y,z) se le llama función escalar de posición.

si a cada punto del espacio podemos asociarle un vector, 

función de la posición, hemos definido un campo vectorial. A la función V (x,y ,z ) se le llama función vectorial de la posición.

Si una función escalar o vectorial depende de dos o más variables escalares, es preciso recurrir para estudiarla al cálculo de sus derivadas parciales con respecto a cada 

una de las variables.
No es posible la derivada de campo escalar sin elegir un vector en cual la dirección se desea calcular al determinar esta derivada

Por ejemplo la función escalar  U (x,y,z)= x+ yz+ z . Para 

calcular la derivada parcial de U(x,y,z) respecto de x derivamos U respecto de x considerando las otras dos variables y,z como constantes.

Un ejemplo en termodinámica una temperatura T tiene una derivada en un proceso Isotérmico (donde la temperatura es constante) en este caso T´vale 0. Yen un proceso Isocorico (donde el volumen es constante) la derivada del temperatura adquiere otro valor distinto de 0. Otro ejemplo puede ser La derivada de el Volumen en un proceso isocorico es 0 puesto que en este proceso el volumen es constante. Mientras que la derivada del volumen en un proceso  isobárico toma un valor diferente de 0, puesto que en este proceso la constante es la presión y el volumen una variable.

           

http://www.itescam.edu.mx/principal/sylabus/fpdb/recursos/r2286.PDF 

http://materias.fi.uba.ar/6201/MosqVectoresacr.pdf

4 Examen. Tres caras de Electricidad

¿QUE ES UN CAMPO ELÉCTRICO?

El campo eléctrico tiene 3 caras:

a) FUERZA: la cual actúa como carga de prueba (ley de Coulomb 1785).

b)TRABAJO: Para transportar la carga de prueba  (ley de Faraday 1831).

c) CARGA SUPERFICIAL: inducida (Ley de Gauss 1834).

Existen tres métodos independientes: para detectar un campo eléctrico:

1° Tener una de prueba (pequeña) y medir vector de aceleración.

En este caso no sabemos cual es la carga que genera el campo ni a que distancia se encuentra, entonces utilizamos una segunda carga de prueba,la cual debe de ser pequeña. Por lo tanto, si sabemos que hay un campo generado por otra carga que no conocemos, ponemos una segunda carga cuyo valor conocemos y medimos la fuerza actuante sobre la misma. 







2° Medir carga de prueba y medir trabajo.

Si conocemos la carga que genera el campo y a qué distancia se encuentra, podemos determinar el campo a una determinada distancia de la misma.





3° Superficie metálica de conductor de carga se desplaza.

Cuando un campo eléctrico atraviesa una superficie, se define al flujo eléctrico como el producto escalar del campo por la superficie. Mide de alguna manera las líneas de campo que atraviesan esa superficie.

Siendo θ el ángulo entre el vector normal al área y el vector campo eléctrico.

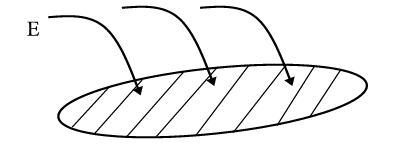
Como las superficies pueden no ser planas y los campos eléctricos no uniformes, se resuelve con una integral. En caso de que el campo sea uniforme se saca E fuera de la integral.

http://www.fisicapractica.com/determinacion-campo.php

5 Examen. Tres caras de magnetismo

¿QUE ES UN CAMPO MAGNÉTICO?

Es la fuerza magnética que proviene de un imán. la fuerza magnética está ilustrada mediante líneas que la representa. a un lado del imán se le llama polo positivo y, a la cara opuesta, polo negativo; la fuerza magnética fluye del lado o polo positivo, en dirección al polo negativo.

EL CAMPO MAGNÉTICO TIENE TRES CARAS:

1° Campo magnetico como vector de fuerza: . Las fuerzas magnéticas son producidas por el movimiento de partículas cargadas, como electrones, lo que indica la estrecha relación entre la electricidad y el magnetismo. Esta cara implica a la ley de Biot y Savart, en la cual  relaciona los campos magnéticos con las corrientes que los crean.  . La obtención del campo magnético resultante de una distribución de corrientes, implica un producto vectorial, y cuando la distancia desde la corriente al punto del campo está variando continuamente, se convierte en un problema de cálculo diferencial.

2° Campo magnético como bi-onda de trabajo, la cual se define con la ley de Gauss, la cual establece que el flujo magnético a través de cualquier superficie cerrada siempre es cero y esta definida con la siguiente integral.

 3° Corriente lineal inducida, magnetización de alambre, esta tercera cara del magnetismo es extensiva puesto que depende del campo magnético  que induce al alambre. Ejemplo: Núcleo magnético. Una espira por la que circula una corriente  i(t) que atraviesa el núcleo:

-Líneas de campo rodean al interior del núcleo

- Para un campo magnético uniforme la integral es 

H(t) 

Donde H es  Campo magnético uniforme de magnitud 

¿COMO DETECTAR UN CAMPO ELÉCTRICO?

Una forma de detectar un campo magnético en un punto del espacio es colocando una aguja imantada, si existe un campo magnético en ese punto la aguja, como consecuencia de las fuerzas magnéticas, gira y se alinea en una dirección determinada en el espacio, la cual es la dirección del campo magnético.

Otra forma de detectar un campo magnético es utilizando limadura de hierro, en presencia de un campo magnético, las limaduras de hierro se convierten en pequeños imanes, los cuales pueden utilizarse como elementos para la detección de un campo magnético. El campo magnético esta orientado en la dirección en que se alinean las limaduras y su intensidad es proporcional a la intensidad de las limaduras.

http://books.google.com.mx/books?id=354FXz7DApwC&pg=PA84&lpg=PA84&dq=como+detectar+un+campo+magnetico&source=bl&ots=g116lE3G-z&sig=KGAoj5abQPaJWXBuYQOu7-kZhsY&hl=es&sa=X&ei=AxpcU4rIFcah8AG7kIGQAQ&ved=0CFgQ6AEwCTgK#v=onepage&q=como%20detectar%20un%20campo%20magnetico&f=true

3. D Axioma de calculo integral

CARBAJAL ESCALONA SILVIA BERENICE.

Borde de Borde siempre es 0 :

La formula mas importante del calculo diferencial es d o d=0, diferencial de diferencial es siempre cero esto significa que borde de borde es cero puesto que "el borde no tiene Borde".

3 C. ¿Cual es nombre mas adecuado para el borde?

CARBAJAL ESCALONA SILVIA BERENICE.

En lo personal el termino mas adecuado es "borde", puesto que este termino define el limite de algo en este caso de una integral o derivada, el cual necesita tener una orientacion, Este termino es mas facil de recordar para el alumno, puesto que lo puede relacionar con distintos ejemplos por ejemplo los bordes de una mesa, estos definen el lugar que ocupa la mesa.  Existen varios bordes:

* Borde de punto orientado= vacio 

* Borde de curva orientada = dos puntos orientada

* Borde de superficie orientado= curva orientada 

3 B. Hermann Weyl en 1918

CARBAJAL ESCALONA SILVIA BERENICE. 

Hermann Weyl 1918  relacionó la integral con los conceptos siguientes: Las propiedades extensivas son aquellas que son independientes de elección de orientación. Mientras que las propiedades intensivas son dependientes de elección de orientación. 

3 A. Operadores diferenciales.

CARBAJAL ESCALONA SILVIA BERENICE

El uso más común del operador diferencial es realizar la derivada en sí misma.

Considerando que la variable es x, la notación más común de éste operador es:

Un operador diferencial vectorial es un operador lineal que actúa sobre campos vectoriales definidos sobre una variedad diferenciables. El operador vectorial nabla es un operador matemático que tiene carácter vectorial, si embargo carece de algunas de las propiedades de las magnitudes vectoriales. En coordenadas cartesianas se expresan por : 

     

Si el operador nabla se aplica escalarmente a un escalar se obtiene el gradiante de dicha función escalar; y si se aplica escalarmente a un vector se obtiene la divergencia de la funciona vectorial.

http://ocw.upm.es/ingenieria-agroforestal/mecanica-y-mecanismos/Contenidos/Teoria/Anejo2.Operadores-diferenciales.pdf

  

3. Calculo diferencial. Integral Parte I

CARBAJAL ESCALONA SILVIA BERENICE.

El calculo diferencial es muy importante para explicar la teoría en termodinámica  y electricidad y magnetismo.

El calculo diferencial es una ciencia que estudia los incrementos o cambios  en las variables. Cada cambio que se 

de es una derivada. Existen dos conceptos fundamentales para el calculo diferencial los cuales son:

* Derivada: Es a la razón de cambio de una variable con respecto a otra. Cada derivada de una función depende de un vector de dirección, por lo tanto cada función tiene varias derivadas en diferentes direcciones. Ejemplo en termodinámica el cambio de temperatura en una dirección de un proceso tiene derivada T´=1, pero en otro proceso puede tener otra derivada de la mima temperatura T´=3. La derivada de una función con respecto así misma es una función constante 1.

*Diferencial: es por definición igual al incremento que experimenta, sin embargo, la diferencial de la variable  no es igual su incremento, la cual se denota con letra "d" Ejemplo diferencial de coordenada dx, en termodinámica diferencial del Volumen cual se denota con letra dV.

La formula mas importante del calculo diferencial es d o d=0, diferencial de diferencial es siempre cero esto significa que borde de borde es cero puesto que "el borde no tiene Borde" 

http://www.fca.unam.mx/docs/apuntes_matematicas/29.%20Diferencial.pdf