CARBAJAL ESCALONA SILVIA BERENICE
miércoles, 21 de mayo de 2014
martes, 20 de mayo de 2014
Exam 9 Integral definitivo
CARBAJAL ESCALONA SILVIA BERENICE
9 A. ¿COMO SE DEFINE CONCEPTO DE INTEGRAL [DEFINITIVO] EN BACHILLERATO?
La integral definida es un concepto
utilizado para determinar el valor de las áreas limitadas por curvas y rectas.
Dado el intervalo [a, b] en el que, para cada uno de sus puntos x, se define
una función f (x) que es mayor o igual que 0 en [a, b], se llama integral
definida de la función entre los puntos a y b al área de la porción del plano
que está limitada por la función, el eje horizontal X y las rectas verticales
de ecuaciones x = a y x = b.
La integral definida de la función entre
los extremos del intervalo [a, b] se denota como:
9 B. INCRUSTACIÓN
Al hablar de incrustacion nos referimos a trazar un plano con dos dimensiones, desde pequeños nos enseñan que estas dos dimensiones se llaman "x" y "y" y las cuales se cruzan en un punto (0,0), como a continuación se ilustra:
La incrustacion de dimensiones aprendidas desde pequeños es errónea puesto que cualquier dimensión que sea trazada en un plano no tendrá un mismo punto de partida con la otra dimensión, puesto que se habla de dos dimensiones diferentes. En este caso se habla de "x" que es un punto de curva y de "y" que es curvas de nivel.
LO CORRECTO ES INCRUSTAR las dimensiones dentro del plano como se muestra:
9 C Presentar su lista privada de los conceptos desde mas importantes para
esta asignatura de TEORIA de Electricidad y Magnetismo.
1°ORIENTACION. Porque sin orientacion no hay borde.
2° BORDE: Sin borde no hay integral
3° Diferencial: d
4° Integral
jueves, 15 de mayo de 2014
EXAMENES 7 C Y 7 D
CARBAJAL ESCALONA SILVIA BERENICE.
7 C COMO DEFINEN EL CONCEPTO DE DIFERENCIAL:
en matematicas:
Sea una funcion y=f(x).
se define como la diferencial de la variable independiente a:
Se define como la diferencial de la variable dependiente a :Esto significa que la diferencial de la variables es por definición igual al incremento que experimenta, sin embargo, la diferencial de la variable no es igual a su incremento.
7 D DECAIMIENTO DE BETA
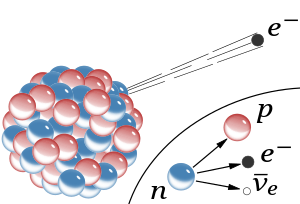
El decaimiento de beta es un proceso mediante el cual un nucleido o núcleo inestable emite una partícula beta (un electrón o positron) para compensar la relación de neutrones y protones del núcleo atómico.Cuando esta relación es inestable, algunos neutrones se convierten en protones. Como resultado de esta mutación, cada neutron emite una partícula beta y un antineutrino electrónico.
La partícula beta puede ser un electrón,
en una emisión beta menos (β–), o un positrón,
en una emisión beta más (β+). La diferencia fundamental entre un
electrón (β–) y la de un positrón (β+) con respecto a la partícula beta
correspondiente es el origen nuclear de aquéllos: no se trata de un electrón
ordinario expulsado de un orbital atómico.
En este tipo de desintegración, el número de neutrones y
protones, o número másico, permanece estable, ya que la cantidad
de neutrones disminuye una unidad y la de protones aumenta así mismo una
unidad. El resultado del decaimiento beta es un núcleo en que el exceso de
neutrones o protones se ha corregido en dos unidades y por tanto resulta más
estable.
7 A y B
CARBAJAL ESCALONA SILVIA BERENICE
7 A. Dar su ejemplo de curvas de niveles
Es necesario saber ¿que es una curva de nivel?
Las curvas de nivel son aplicadas en el área de la
Ingeniería para mostrar en el plano curvas isotermas o líneas equipotenciales, por mencionar algunas. En las curvas
Isotermas la líneas continuas enlazan la misma temperatura en la zona.
DEFINICIÓN Curva de nivel
El conjunto de puntos (x, y) en el plano donde una función de dos variables independientes tiene un valor constante f(x, y) = c, es una curva de nivel de f.
Solución La función dada representa la superficie de
un paraboloide elíptico abierto hacia arriba.
Si (x, y) = (0, 0)
entonces z = –5. Las curvas de
nivel son elipses.
7 B. Presentar su privado ejemplo de evaluacion gra camente de un campo
vectorial (de
echas) con una forma-onda (con crestes) en tres puntos.
CORRECIÓN 3D. BORDE NO TIENE BORDE. DEFINICIÓN DE INTEGRAL
CARBAJAL ESCALONA SILVIA BERENICE
En el bachillerato nos muestran la definición de integral como:
LA DEFINICIÓN CORRECTA DE LA INTEGRAL ES:
CADA VEZ QUE SE INTEGRA SOBRE "BORDE DE ALGO" EL BORDE PASA HACER DIFERENCIAL.
Axioma de calculo integral: borde no
tiene borde.
El borde (limite, frontera,etc.) no puede tener un borde puesto que disminuye la dimensión y es por esta razón que siempre que se tenga borde de borde, diferencial de diferencial sera cero.
sábado, 10 de mayo de 2014
6 B. Reglas de Leibniz.
Suscribirse a:
Entradas (Atom)

















 —> donde f(
—> donde f(